Calcule el número total de combinaciones permitiendo repetición y seleccionando r elementos de n elementos.

Ingrese el número total (n) y el número seleccionado (r) y haga clic en el botón "Calcular combinaciones" para calcular el número total de combinaciones que se extraerán permitiendo repetición y seleccionando r piezas de n piezas Calcular y mostrar. .

También muestra cómo calcular el número total de combinaciones.

Introduzca Número total y Numero seleccionado como números enteros positivos hasta 10,000.

La combinación es la selección de varias cosas diferentes que se pueden distinguir.

La combinación seleccionada al permitir repetición se llama Combinación.

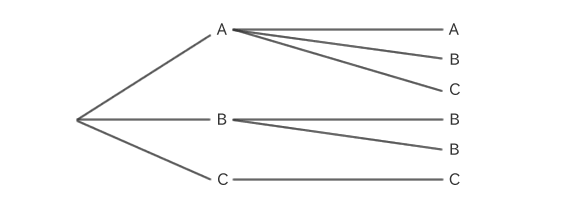
Por ejemplo, supongamos que elige dos de los tres alfabetos A, B y C.

Puedes elegir el mismo artículo varias veces, por lo que hay 6 formas de elegir: AA, AB, AC, BB, BC, CC.

A diferencia de las permutaciones, las combinaciones no consideran el orden, por lo que combinaciones como AB y BA que son iguales después de ser reorganizadas se consideran una.

Si elige dos de A, B y C, la combinación se verá así en un dendrograma.

Al calcular el número total de Combinaciones con repetición, considere usar círculos y divisores.

Por ejemplo, digamos que hay tres alfabetos, A, B y C, y quieres elegir cuatro de ellos y pensar en una combinación.

Encierra en un círculo los cuatro alfabetos para elegir (〇) y, como hay tres tipos de alfabetos, prepara dos divisores (｜) y alinéalos.

Alinea el círculo y el divisor y llámalo ABC desde la izquierda del divisor.

Por ejemplo, 〇〇｜〇｜〇 es una combinación de AABC.Además, en el caso de 〇｜｜〇〇〇, es una combinación de ACCC.

El número total de permutaciones de este círculo y divisor es el número total de Combinaciones con repetición.

¡El número total de permutaciones de círculos y particiones es 6!, y no hay distinción entre círculos y particiones, así que divida por (4! × 2!).

Por tanto, el número total de combinaciones es 6!4!2! = 15.

Por lo tanto, el número total de combinaciones extraídas al seleccionar r elementos de n elementos con repetición permitido se puede calcular como (r+n−1)!r!(n−1)!.